|
Menu

Links
nils-uni@bluemer.name


|
|
Prof. Dr. Nils Blümer |
|
Attention: these pages are mostly outdated! For current information on Nils Blümer, see web pages at the KU.
Modern numerical methods in solid state physics
Lecture in summer semester 2007
N. Blümer
Lecture hours: 3 V + 1 Ü (lectures + tutorials)
Time and Place: Mondays 1615-1745, Thursdays 830-10 in Seminarraum D (Staudingerweg 9, 01-217)
Target group: physics students after Vordiplom, PhD students
Univis entry: see list of lectures by N. Blümer in SS 2007
Consultation hours: after lectures or by appointment
Note: No english version this time.
Inhalt / Notizen zur Vorlesung
- Vorlesung 1 (26.04.2007)
- Vorlesung 2 (30.04.2007) num-meth-ss07-v02.pdf
- Fortsetzung I.1
- Beispiel Datenanalyse (online per Beamer; Daten und pdf-file siehe unten)
- Vorgriff Metropolis-Algorithmus (zu Aufgabenblatt 1)
- Vorlesung 3 (03.05.2007) num-meth-ss07-v03.pdf
- I.2 Metropolis-Monte-Carlo Methode (simple Monte-Carlo, Monte-Carlo mit Gewichtung (importance sampling), Markov-Ketten-Monte-Carlo)
- Vorlesung 4 (07.05.2007) num-meth-ss07-v04.pdf
- Markov-Ketten-Monte-Carlo, detailliertes Gleichgewicht, Metropolis-Algorithmus
- I.3 Statistische Physik im kanonischen Ensemble
- Thermodynamische Erwartungswerte, Phasenübergänge, kritische Exponenten
- Besprechung Aufgabenblatt 1 (10.05.2007)
- Vorlesung 5 (14.05.2007) num-meth-ss07-v05.pdf
- I.4 Ising-Modell
- Aufgabe: MC-Simulation des 2D Ising-Modells
- Vorlesung 6 (21.05.2007) num-meth-ss07-v06.pdf
- Kritische Temperaturen und kritische Exponenten des Ising-Modells
- I.5 Finite-size scaling
- Binder-Kumulante, Extraktion des kritischen Exponenten β
- Besprechung Aufgabenblatt 2 - MC-Simulation Ising-Modell (24.05.2007), Musterlösung: comp-sim_hw4.pdf
- Vorlesung 7 (Sondertermin 25.05.2007) num-meth-ss07-v07.pdf
- I.6 Monte-Carlo-Simulationen mit Cluster-Updates
- Swendsen-Wang-Algorithmus, Wolf-Algorithmus
- Wolff-MC-Resultate für das 2D Ising-Modell: comp-sim_Wolff_p.pdf
- Vorlesung 8 (04.06.2007) num-meth-ss07-v08.pdf
- Start Kapitel II - Exakte Diagonalisierung
- II.1 Matrixdarstellung des Heisenberg-Modells: Historie Heisenberg-Modell, Grenzfälle/Verallgemeinerungen, Matrixdarstellung
- Beispiel: 2 Spins (offene Randbedingungen)
- II.2 Mathematische Exkurs: Eigenwertprobleme: Existenz von (Rechts-)Eigenvektoren, Matrix-Definitionen, Ähnlichkeitstransformationen (allgemein bzw. unitär), Sätze zu Normalformen und Diagonalisierbarkeit von Matrizen
- Besprechung Aufgabenblatt 3 - von-Mises-ED-Verfahren (11.06.2007)
- Vorlesung 9 (14.06.2007) num-meth-ss07-v09.pdf
- Nachtrag: Matrizen mit vollständiger Eigenbasis versus normale Matrizen - Vergleich anhand von Zufallsmatrizen
- II.3 Reduktion des Hilbertraums (vor ED)
- Symmetrien des Heisenberg-Modell: z-Komponente des Gesamtspins (mz), Spin-Umkehr, Spiegelung, Translation (periodische Randbedingungen), Diagonalspiegelung (d>1)
- Beispiele: Heisenberg-Modell für N=2 und N=4
- Vorlesung 10 (15.06.2007) num-meth-ss07-v10.pdf
- Vollständige analytische Lösung des 4-Spin-Heisenberg-Modells für periodische und offene Randbedingungen.
- Vorlesung 11 (18.06.2007) num-meth-ss07-v11.pdf
- II.4 Numerische Verfahren zur vollständigen Bestimmung von Eigenwerten und (optional) Eigenvektoren von symmetrischen Matrizen
- 1. Naive Strategie über charakteristisches Polynom
- 2. Vektoriteration nach von Mises und inverse Iteration nach Wielandt
- 3. Iterative Diagonalisierung mit Jacobi-Rotationen
- Vorlesung 12 (21.06.2007) num-meth-ss07-v12.pdf
- 4. Vollständige Tridiagonalisierung symmetrischer Matrizen nach Givens
- 5. Vollständige Tridiagonalisierung symmetrischer Matrizen mit Householder-Transformationen
- II.5 Bestimmung aller Eigenwerte und (optional) Eigenvektoren von symmetrischen Tridiagonalmatrizen
- 1. Bestimmung über charakteristisches Polynom
- Besprechung Aufgabenblatt 4 (25.06.2007) - Musterlösung: num-meth-ss07-hw4.pdf
- Vorlesung 13 (28.06.2007) num-meth-ss07-v13.pdf
- 2. Iterative Diagonalisierung einer Tridiagonalmatrix mittels QR bzw. QL-Zerlegung
- Beispiel im Detail (anhand Mathematica Notebook)
- Implementierung (pdf-Listing): ED_tridiag.c.pdf
- Vorlesung 14 (02.07.2007) num-meth-ss07-v14.pdf
- II.6 Partielle Tridiagonalisierung mit dem Lanczos-Algorithmus
- Krylov-Unterräume
- Implementierung des Lanczos-Algorithmus und Anwendung auf AF Heisenberg-Spinkette: num-meth-ss07-Lanczos.pdf
- Beamer-Forschungsvortrag (05.07.2007)
- Vorlesung 15 (09.07.2007) num-meth-ss07-v15.pdf
- III Quanten-Monte-Carlo Simulationen
- III.1 Klassifikation von Quanten-Monte-Carlo-Methoden
- III.2 Pfadintegral-Quanten-Monte-Carlo (PIMC)
- Vorlesung 16 (12.07.2007) num-meth-ss07-v16.pdf
- Fortsetzung PIMC
- Vorstellung: ALPS - Algorithms and Libraries for Physics Simulations
- Vorlesung 17 (16.07.2007) num-meth-ss07-v17.pdf
- III.3 Weltlinien-Quanten-Monte-Carlo
- Aufgabe WL-QMC für XXZ-Modell
- Vorlesung 18 (19.07.2007) num-meth-ss07-v18.pdf
- Observablenbestimmung bei Weltlinien-Quanten-Monte-Carlo, speziell: Energie
- Probleme bei lokalen WL-Updates
- III.4 WL-QMC mit Schleifen(loop)-Updates
- Abbildung auf 6-Vertex-Modell, Loop-Auswahl, globale Update-Möglichkeit
- Schleifen-Graphen; Loop-Algorithmen analog zu Swendson-Wang- bzw. Wolff-Algorithmen für Ising-Modell
- Seminarvortrag (09.08.2007)
- Vortrag Das ALPS-Projekt: Vorstellung und Anwendung von Konstantin Koschke und Daniel Reith
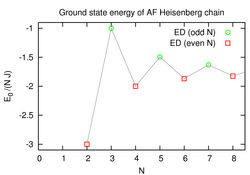
- Exakte Diagonalisierung für AF Heisenberg-Kette
- QMC mit Loop-Algorithmus für AF Heisenberg-Modell in 1, 2 und 3 Dimensionen
Aufgabenblätter / Beispiele / Computerprogramme
- 30.04.2007 Beispiel Datenanalyse: analysieren Sie die folgenden Beispieldaten
- set 1 (10, 100, 1000, 10000 numbers)
- set 2 (10, 100, 1000, 10000 numbers)
- set 3 (10, 100, 1000, 10000 numbers)
- set 4 (10, 100, 1000, 10000 numbers)
- set 5 (10, 100, 1000, 10000 numbers)
- set 6 (10, 100, 1000, 10000 numbers)
- Musterlösung: comp-sim_hw2.pdf; Auswahl von gnuplot-Sourcefiles: stats_set1_trace.gnu, stats_set1_hist_corr.gnu, stats_set4_hist_corr.gnu
- 30.04.2007 1. Aufgabenblatt: Metropolis Monte-Carlo (Abgabetermin: 10.05.2007)
- 14.05.2007 Monte-Carlo-Simulation des 2D-Ising-Modells (Abgabetermin: 24.05.2007)
- Schreiben Sie ein Metropolis-Monte-Carlo-Programm zur Berechnung von Energie und Magnetisierung des Ising-Modells in 2 Raumdimensionen. Dabei dürfen Sie das unten verlinkte Templat benutzen.
- Berechnen Sie Mittelwerte E(T) und |M(T)| (mit Fehlerbalken) in einem sinnvollen Temperaturbereich für Gitter mit linearer Ausdehnung zwischen 4 und etwa 20-40.
- Tragen Sie die Binder-Kumulante U4(T)=1-⟨m4⟩/(3⟨m2⟩2) für verschiedene Gittergrößen auf und bestimmen Sie aus dem asymptotischen Schnittpunkt die kritische Temperatur Tc.
- Optional: Bestimmen Sie die spezifische Wärme und die magnetische Suszeptibilität bei ausgewählten Temperaturen.
- 24.05.2007 3. Aufgabenblatt: Exakte Diagonalisierung (Abgabetermin: 11.06.2007)
- 14.06.2007 4. Aufgabenblatt: Grundzustandseigenschaften der antiferromagnetischen Heisenbergkette (Abgabetermin: 21.06.2007)
- 16.07.2007 5. Aufgabenblatt: Weltlinien-QMC (Abgabetermin: 26.07.2007)
- Implementieren Sie die Weltlinien-QMC-Methode mit lokalen Updates (heat bath-Akzeptanzregel) für das XXZ-Modell (cf. Vorlesung 17).
- Extrapolieren Sie die Energie E(T) der AF-Heisenberg-Kette (Jx=Jz=1) mit L=8 Spins jeweils bei fester Temperatur zu verschwindender Diskretisierung (getrennt für Spinsektoren).
- Tragen Sie jeweils auch die Autokorrelationszeit von Energie und NN-Spinkorrelation auf.
- Schätzen Sie für L=8 die Grundzustandsenergie ab.
- Optional: testen Sie den Algorithmus für große Systeme (z.B. 50 Spins)
- Vergleichsergebnisse für L=8 und T=1/10:
Beispielprogramme und Tools:
|