Auswahlmenü

	Startseite
	CV
	Präsentationen
	Veröffentlichungen
	Doktorarbeit
	Vorlesungen
	WS2014 SS2013 WS2012 SS2012 WS2011 SS2011 WS2010 SS2010 WS2009 SS2009 WS2008 SS2008 WS2007 SS2007 WS2006 SS2006 WS2005 SS2005
	Evaluation
	Computing

Links

Stundenzahl: 3 V + 1 Ü

Zeit und Ort: Mo 16¹⁵-17⁴⁵ Uhr, Do 8³⁰-10⁰⁰ Uhr im Seminarraum D (Staudingerweg 9, 01-217)

Zielgruppe: Studierende im Hauptstudium, Doktoranden

Univis-Eintrag: siehe Liste der Lehrveranstaltungen von N. Blümer im SS 2007

Sprechstunde: Do nach der Vorlesung und nach Vereinbarung

Inhalt / Notizen zur Vorlesung

• Vorlesung 1 (26.04.2007)
  • Teilnehmer-Fragebogen: num-meth-ss07-Fragebogen.pdf
  • Inhaltsübersicht: num-meth-ss07-Inhalt.pdf
  • Start Kapitel I - Monte-Carlo-Simulationen des Ising-Modells
  • I.1 Datenanalyse von Zeitreihen: num-meth-ss07-v01.pdf
• Vorlesung 2 (30.04.2007) num-meth-ss07-v02.pdf
  • Fortsetzung I.1
  • Beispiel Datenanalyse (online per Beamer; Daten und pdf-file siehe unten)
  • Vorgriff Metropolis-Algorithmus (zu Aufgabenblatt 1)
• Vorlesung 3 (03.05.2007) num-meth-ss07-v03.pdf
  • I.2 Metropolis-Monte-Carlo Methode (simple Monte-Carlo, Monte-Carlo mit Gewichtung (importance sampling), Markov-Ketten-Monte-Carlo)
• Vorlesung 4 (07.05.2007) num-meth-ss07-v04.pdf
  • Markov-Ketten-Monte-Carlo, detailliertes Gleichgewicht, Metropolis-Algorithmus
  • I.3 Statistische Physik im kanonischen Ensemble
  • Thermodynamische Erwartungswerte, Phasenübergänge, kritische Exponenten
• Besprechung Aufgabenblatt 1 (10.05.2007)
• Vorlesung 5 (14.05.2007) num-meth-ss07-v05.pdf
  • I.4 Ising-Modell
  • Aufgabe: MC-Simulation des 2D Ising-Modells
• Vorlesung 6 (21.05.2007) num-meth-ss07-v06.pdf
  • Kritische Temperaturen und kritische Exponenten des Ising-Modells
  • I.5 Finite-size scaling
  • Binder-Kumulante, Extraktion des kritischen Exponenten β
• Besprechung Aufgabenblatt 2 - MC-Simulation Ising-Modell (24.05.2007), Musterlösung: comp-sim_hw4.pdf
• Vorlesung 7 (Sondertermin 25.05.2007) num-meth-ss07-v07.pdf
  • I.6 Monte-Carlo-Simulationen mit Cluster-Updates
  • Swendsen-Wang-Algorithmus, Wolf-Algorithmus
  • Wolff-MC-Resultate für das 2D Ising-Modell: comp-sim_Wolff_p.pdf
• Vorlesung 8 (04.06.2007) num-meth-ss07-v08.pdf
  • Start Kapitel II - Exakte Diagonalisierung
  • II.1 Matrixdarstellung des Heisenberg-Modells: Historie Heisenberg-Modell, Grenzfälle/Verallgemeinerungen, Matrixdarstellung
  • Beispiel: 2 Spins (offene Randbedingungen)
  • II.2 Mathematische Exkurs: Eigenwertprobleme: Existenz von (Rechts-)Eigenvektoren, Matrix-Definitionen, Ähnlichkeitstransformationen (allgemein bzw. unitär), Sätze zu Normalformen und Diagonalisierbarkeit von Matrizen
• Besprechung Aufgabenblatt 3 - von-Mises-ED-Verfahren (11.06.2007)
• Vorlesung 9 (14.06.2007) num-meth-ss07-v09.pdf
  • Nachtrag: Matrizen mit vollständiger Eigenbasis versus normale Matrizen - Vergleich anhand von Zufallsmatrizen
  • II.3 Reduktion des Hilbertraums (vor ED)
  • Symmetrien des Heisenberg-Modell: z-Komponente des Gesamtspins (m_z), Spin-Umkehr, Spiegelung, Translation (periodische Randbedingungen), Diagonalspiegelung (d>1)
  • Beispiele: Heisenberg-Modell für N=2 und N=4
• Vorlesung 10 (15.06.2007) num-meth-ss07-v10.pdf
  • Vollständige analytische Lösung des 4-Spin-Heisenberg-Modells für periodische und offene Randbedingungen.
• Vorlesung 11 (18.06.2007) num-meth-ss07-v11.pdf
  • II.4 Numerische Verfahren zur vollständigen Bestimmung von Eigenwerten und (optional) Eigenvektoren von symmetrischen Matrizen
  • 1. Naive Strategie über charakteristisches Polynom
  • 2. Vektoriteration nach von Mises und inverse Iteration nach Wielandt
  • 3. Iterative Diagonalisierung mit Jacobi-Rotationen
• Vorlesung 12 (21.06.2007) num-meth-ss07-v12.pdf
  • 4. Vollständige Tridiagonalisierung symmetrischer Matrizen nach Givens
  • 5. Vollständige Tridiagonalisierung symmetrischer Matrizen mit Householder-Transformationen
  • II.5 Bestimmung aller Eigenwerte und (optional) Eigenvektoren von symmetrischen Tridiagonalmatrizen
  • 1. Bestimmung über charakteristisches Polynom
• Besprechung Aufgabenblatt 4 (25.06.2007) - Musterlösung: num-meth-ss07-hw4.pdf
• Vorlesung 13 (28.06.2007) num-meth-ss07-v13.pdf
  • 2. Iterative Diagonalisierung einer Tridiagonalmatrix mittels QR bzw. QL-Zerlegung
  • Beispiel im Detail (anhand Mathematica Notebook)
  • Implementierung (pdf-Listing): ED_tridiag.c.pdf
• Vorlesung 14 (02.07.2007) num-meth-ss07-v14.pdf
  • II.6 Partielle Tridiagonalisierung mit dem Lanczos-Algorithmus
  • Krylov-Unterräume
  • Implementierung des Lanczos-Algorithmus und Anwendung auf AF Heisenberg-Spinkette: num-meth-ss07-Lanczos.pdf
• Beamer-Forschungsvortrag (05.07.2007)
  • Zur Einstimmung: Vortrag Quantum Monte Carlo simulations of strongly correlated electron systems within dynamical mean-field theory
• Vorlesung 15 (09.07.2007) num-meth-ss07-v15.pdf
  • III Quanten-Monte-Carlo Simulationen
  • III.1 Klassifikation von Quanten-Monte-Carlo-Methoden
  • III.2 Pfadintegral-Quanten-Monte-Carlo (PIMC)
• Vorlesung 16 (12.07.2007) num-meth-ss07-v16.pdf
  • Fortsetzung PIMC
  • Vorstellung: ALPS - Algorithms and Libraries for Physics Simulations
• Vorlesung 17 (16.07.2007) num-meth-ss07-v17.pdf
  • III.3 Weltlinien-Quanten-Monte-Carlo
  • Aufgabe WL-QMC für XXZ-Modell
• Vorlesung 18 (19.07.2007) num-meth-ss07-v18.pdf
  • Observablenbestimmung bei Weltlinien-Quanten-Monte-Carlo, speziell: Energie
  • Probleme bei lokalen WL-Updates
  • III.4 WL-QMC mit Schleifen(loop)-Updates
  • Abbildung auf 6-Vertex-Modell, Loop-Auswahl, globale Update-Möglichkeit
  • Schleifen-Graphen; Loop-Algorithmen analog zu Swendson-Wang- bzw. Wolff-Algorithmen für Ising-Modell
• Seminarvortrag (09.08.2007)
  • Vortrag Das ALPS-Projekt: Vorstellung und Anwendung von Konstantin Koschke und Daniel Reith
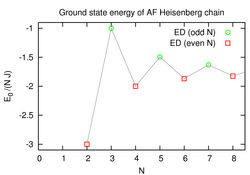
  • Exakte Diagonalisierung für AF Heisenberg-Kette
  • QMC mit Loop-Algorithmus für AF Heisenberg-Modell in 1, 2 und 3 Dimensionen

Aufgabenblätter / Beispiele / Computerprogramme

• 30.04.2007 Beispiel Datenanalyse: analysieren Sie die folgenden Beispieldaten
  • set 1 (10, 100, 1000, 10000 numbers)
  • set 2 (10, 100, 1000, 10000 numbers)
  • set 3 (10, 100, 1000, 10000 numbers)
  • set 4 (10, 100, 1000, 10000 numbers)
  • set 5 (10, 100, 1000, 10000 numbers)
  • set 6 (10, 100, 1000, 10000 numbers)
  • Musterlösung: comp-sim_hw2.pdf; Auswahl von gnuplot-Sourcefiles: stats_set1_trace.gnu, stats_set1_hist_corr.gnu, stats_set4_hist_corr.gnu
• 30.04.2007 1. Aufgabenblatt: Metropolis Monte-Carlo (Abgabetermin: 10.05.2007)
  • Musterlösung: uebung1_lv.pdf, benutzt lv_ueb1.cpp.
• 14.05.2007 Monte-Carlo-Simulation des 2D-Ising-Modells (Abgabetermin: 24.05.2007)
  • Schreiben Sie ein Metropolis-Monte-Carlo-Programm zur Berechnung von Energie und Magnetisierung des Ising-Modells in 2 Raumdimensionen. Dabei dürfen Sie das unten verlinkte Templat benutzen.
  • Berechnen Sie Mittelwerte E(T) und |M(T)| (mit Fehlerbalken) in einem sinnvollen Temperaturbereich für Gitter mit linearer Ausdehnung zwischen 4 und etwa 20-40.
  • Tragen Sie die Binder-Kumulante U₄(T)=1-⟨m⁴⟩/(3⟨m²⟩²) für verschiedene Gittergrößen auf und bestimmen Sie aus dem asymptotischen Schnittpunkt die kritische Temperatur T_c.
  • Optional: Bestimmen Sie die spezifische Wärme und die magnetische Suszeptibilität bei ausgewählten Temperaturen.
• 24.05.2007 3. Aufgabenblatt: Exakte Diagonalisierung (Abgabetermin: 11.06.2007)
  • Weitere Hinweise: siehe Übungs-Seite
• 14.06.2007 4. Aufgabenblatt: Grundzustandseigenschaften der antiferromagnetischen Heisenbergkette (Abgabetermin: 21.06.2007)
  • Code zur exakten Diagonalisierung: siehe unten.
  • Hamilton-Matrizen für kleine Systeme (zu Vergleichszwecken; Zahl in 2. Zeile gibt jeweils Dimension an):
    • N=1: Heisenberg_AF_N1_m1.dat
    • N=2: Heisenberg_AF_N2_m2.dat, Heisenberg_AF_N2_m0.dat
    • N=3: Heisenberg_AF_N3_m3.dat, Heisenberg_AF_N3_m1.dat
    • N=4: Heisenberg_AF_N4_m4.dat, Heisenberg_AF_N4_m2.dat, Heisenberg_AF_N4_m0.dat
    • N=5: Heisenberg_AF_N5_m5.dat, Heisenberg_AF_N5_m3.dat, Heisenberg_AF_N5_m1.dat
    • N=6: Heisenberg_AF_N6_m6.dat, Heisenberg_AF_N6_m4.dat, Heisenberg_AF_N6_m2.dat, Heisenberg_AF_N6_m0.dat
    • N=7: Heisenberg_AF_N7_m7.dat, Heisenberg_AF_N7_m5.dat, Heisenberg_AF_N7_m3.dat, Heisenberg_AF_N7_m1.dat
    • N=8: Heisenberg_AF_N8_m8.dat, Heisenberg_AF_N8_m6.dat, Heisenberg_AF_N8_m4.dat, Heisenberg_AF_N8_m2.dat, Heisenberg_AF_N8_m0.dat
  • Zwischenergebnisse für kleine Systeme:

    # energies E/N and NN correlations of AF Heisenberg model
     2    -3.00000    -1.00000
     3    -1.00000    -0.33333
     4    -2.00000    -0.66667
     5    -1.49443    -0.49814
     6    -1.86852    -0.62284
     7    -1.63153    -0.54384
     8    -1.82555    -0.60852
    

    
  • Codes zur exakten Diagonalisierung: siehe unten.
• 16.07.2007 5. Aufgabenblatt: Weltlinien-QMC (Abgabetermin: 26.07.2007)
  • Implementieren Sie die Weltlinien-QMC-Methode mit lokalen Updates (heat bath-Akzeptanzregel) für das XXZ-Modell (cf. Vorlesung 17).
  • Extrapolieren Sie die Energie E(T) der AF-Heisenberg-Kette (J_x=J_z=1) mit L=8 Spins jeweils bei fester Temperatur zu verschwindender Diskretisierung (getrennt für Spinsektoren).
  • Tragen Sie jeweils auch die Autokorrelationszeit von Energie und NN-Spinkorrelation auf.
  • Schätzen Sie für L=8 die Grundzustandsenergie ab.
  • Optional: testen Sie den Algorithmus für große Systeme (z.B. 50 Spins)
  • Vergleichsergebnisse für L=8 und T=1/10:
    • ...